This is a little advanced for my age level, but might be interesting to advanced 5th graders and Middle School students.
Start with this picture of a garage in Waterbury, CT.
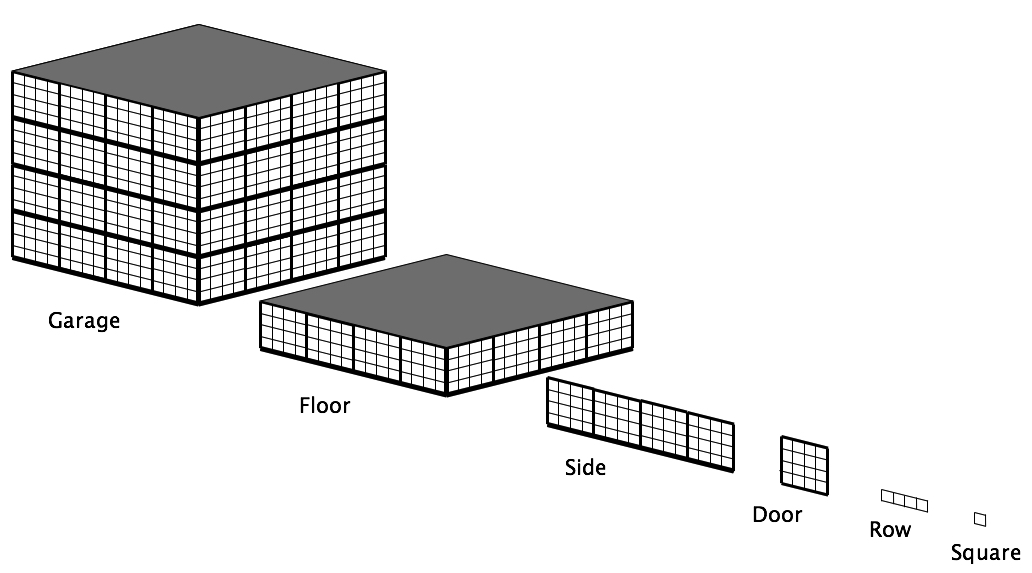
This is the Powers of Four Garage Door, and can be used as the basis for an exploration into both powers of 4, and Base 4 numbers.
When we extend it, it can also be used as the departure for exploring Base 4. This drawing demonstrates the number of squares if the front is reproduced onto all 4 sides off the building.
Now imagine the owners decide they want to expand vertically.
Below is the expansion of the numbers above.
How would you name these numbers? The problem is that we need to assign the numbers 1, 10, 100, etc. to these groups of squares. But it doesn’t make much sense to call them “ten,” “1 hundred,” and so on, because those words have specific meanings relating to Base 10. Perhaps there needs to be another naming system.
Maybe we should call them what they are – the object that they name, in other words.
Let’s say that someone decided to paint the exterior of this approximate cube, and knocked off for the day after painting 1 floor, 2 sides, 3 doors, 2 rows, and 1 square.
In our familiar notation, that would be 12321: 1 floor, 2 sides, 3 doors, 2 rows, and 1 square.
Perhaps we could name it in the same way we would name a similar number in Base 10.
Could it be… 12 sides, 3 doors, 21 squares? … or, 123 doors, 21 squares? … Where would the commas go? As an elementary teacher, I'm not very familiar with teaching children to work in other bases, so I guess I'll bow out at this point.